今回のお題
カオス(2):振り子と陥穽(ver.1.0)
こんなおもちゃ(というかインテリアというか)をときどき見かける。

ちなみに、この写真に写ってるのは、僕が能勢電鉄日生中央駅前のフリーマーケットで100円で手にいれたもの。一見簡単な作りなのだけど、これがなかなか複雑な動きで、ついいつまででもぼーっと見つづけてしまう。こういうのは危険だ。これが規則正しく揺れるだけのものだったとしたら、見ててもすぐに飽きてしまうだろうし、かといって、まったくのでたらめというのもまた、それはそれで面白くないのだと思う。適当に期待を裏切った動きをしてくれるところが、ついつい見とれてしまう理由に違いない。まったくのでたらめではないはずなのに先の予測がつかないというところが、おもちゃやインテリアにちょうどいいのだろうね。カオスの特性がこんなところに利用されてるわけだ。
さて、このおもちゃ、インテリア用だけあってしゃれた格好に作ってはあるけれど、余分なものを剥ぎとってつきつめちゃうと、振り子の中にもうひとつ振り子がついているだけ、つまり単なる二重の振り子にすぎない。もちろん、それだけでは摩擦のためにすぐに止まってしまうから、いつまでも揺れ続けるように電池で駆動している。このしかけがまた磁石とコイルとトランジスタを使った巧妙なものなのだけど、それは今回のテーマじゃないので省略。ちなみに電気式の振り子時計にも同じしくみのものがある。気になる人は自分で分解してみてください。でも、元に戻せなくなってもしらないよ。
軸受けを工夫して摩擦を小さくしてやれば、電池で駆動しなくても、見て楽しめる程度には長く動いてくれるものを作れる。もちろん、ちょっと想像すればわかる通り、振り子一個だけでは複雑なことはなにも起きない。振り子はただ規則正しく揺れるだけだ。なにしろ、振り子の等時性といえば、かのガリレオ・ガリレイが発見した由緒正しい法則なのだから。要するに、振り子を二重にしたところが、今のおもちゃの肝というわけだね。だから、デザインは二の次にしてとにかく複雑な動きを見たいということなら、振り子の先にもう一個振り子をつけたもので充分。ただし、振り子とはいっても、ただ左右に揺れるだけじゃなくて、ぐるぐる回れるようになってないと面白くならない。だから、天井から糸で錘を吊ったんじゃあだめ。糸じゃなくて棒、天井じゃなくて回転できる支点が必要だ。
ためしにそういう振り子を作って、小さく振ってみよう。
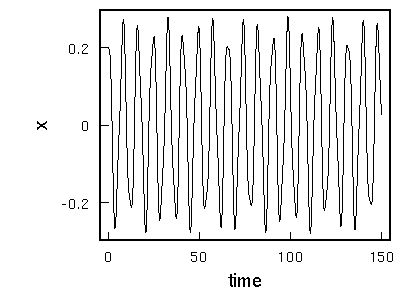
図は、二重振り子の先端の横位置をプロットしたもの。真下を向いてれば0ね。といっても、本物の振り子で実験してる暇がなかったので、残念ながらこれは計算機シミュレーションね。振り子全体がどう動くかは、例によって
JAVAでシミュレーション・プログラムを作ったので、眺めてみてください。一個の振り子よりは多少複雑とはいえ、これは振り子ふたつが”共鳴”しているだけで、予測できないほど複雑な動きにはならない。もちろん、カオスじゃない。
ところが、これを非常に大きく振ると、驚くべきことがおきる。それこそ、一番高いところあたりまで持ち上げて手を離してみたときのグラフはこんな感じ。
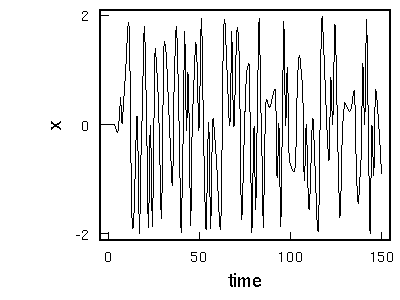
ああ、ずいぶんでたらめな動きになってしまった。これは立派なカオスだ。こちらも、
シミュレーションで見てみると、たしかに予測を裏切る複雑な動きをする。油断すると、思わずぼーっと眺めてしまうから、危険だよ。要するに、振幅がある程度大きくないとカオスにはならないわけだね。
さて、この二重振り子はニュートン力学の法則に従って動いている。ニュートン力学なので、ニュートンの運動方程式とよばれるひと組の方程式が、この振り子の運動を完全に決めている。実際、上のシミュレーションもニュートンの運動方程式を計算しているだけだ。ニュートン力学では、今この瞬間での振り子の位置と速度を決めてやれば、今後未来永劫に至るまでの振り子の運動が、完全に決定してしまい、そこに偶然の要素はなんらふくまれない。その意味で、このシステムは前回のローレンツ方程式と同じように、決定論的でありながら予測不能な運動をするシステムになっている。ニュートン力学から非常に複雑な運動が生じ得ることは、既に100年も前にポアンカレが指摘していた。二重振り子はその中でも特に単純なシステムの例だ。なんたって、振り子ふたつだけだからね。力だって重力だけだもん。
ときどき、「カオスはニュートン以来のパラダイムを覆す」といったセンセーショナルな文章を見かける。その真意がどこにあるのか、僕にはわからないけど、少なくとも、ニュートン力学がカオスのために無効になってしまったりはしていない。そういう印象を与える本があったとしたら、それはたぶんちょっとばかり書きすぎなのだと思う。たかだか二重振り子程度のシステムがカオスを生み出すのだから、実はカオスというのはかなりありふれたものなのだね。むしろ、ニュートン力学に従うシステムの殆どすべてはカオスを生じると言っちゃってもいいくらいだ。だから、ニュートンは今でも健在で、カオスを生み出し続けている。なにかが覆されたのだとすると、それは”世界とは究極的に予測可能なものだ”という期待なのだと思う。ラプラスの悪魔は100年ばかり前に死んでしまっていたというわけ。うん、でも、それを誰もが実感できるようになったのは、コンピュータシミュレーションが手軽に見られるようになったおかげかもしれない。

ちなみに、これは僕がアクリルを切って作った二重振り子の写真。せっかく作ったはいいけど、摩擦をなめてかかったもんだから、ちょっと動いたらすぐに止まっちゃうんだ。格好はいいんだけどね。悔しいなあ。実際に作るとなると、摩擦が落し穴になっちゃうね。やっぱり、ちゃんとベアリング式の軸受けにしないとだめなんだな。こういうのって、小学生の夏休みの工作なんかにいいかもしれないね。別に理屈なんかわかんなくてもいいんだし。というわけで、実際に作ってみた、という読者のかた、おられたらメールください。
(木口まこと)