表紙の科学
第一回:あくまでソリトン

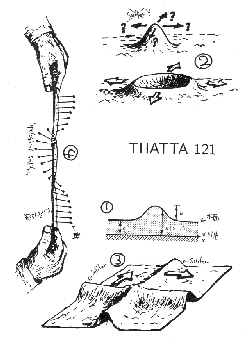
1834年にJ.S.Russelがテムズ河の支流を眺めているとき、高さ1フィートばかりの水面の盛り上がりを発見し、馬で1マイルばかり追跡した、という記述が残されている。この盛り上がりは、形を変えずに時速8マイルほどの速度を保って進んでいった。これが、おそらくはソリトンが記録された最初の例であろう。そのソリトンは横から見るとたぶん図1のようなものだったと想像される。これは浅い水の波を記述するKdV方程式から導かれる孤立波である。この孤立波は変形せず一定速度で進行する。このような孤立波が海面に発生することもあり、ときには横方向には数十キロにわたって伸びたものができる。
ソリトンが安定して存在できる理由については、よく「分散と非線型性がつりあう」などとわけのわからない表現で説明される。分散というのは進行速度に関係しているので、なにかとつりあっている以上、進行速度は一定である。逆に言うと、進行速度が変化するものは「分散と非線型性がつりあ」っていないので、ソリトンにはならないのである。
さて、このような横に長く(水路の幅いっぱいに)伸びたソリトンでは面白くないので、水面(濃度界面でもいいが、とにかく2次元面)のどの方向から見ても孤立したソリトンが作れないかという疑問が湧く。たとえば図2のようなものが、水面の完全な孤立波として期待されるものだろう。残念ながら、このタイプが水面で形を変えずに進行することはありえず、必ず広がって消滅してしまう。図3のようにふたつの横に長いソリトンが交差して、それぞれ一定速度で進行するなら、その交点にできる盛り上がりは形を変えないかもしれない。水上ではおそらくこれが唯一の可能性だろう。ただし、この方法で複数の孤立波を作ったとしても、互いに勝手に動き回ることはできない。
図4のタイプは「位相ソリトン」とよばれ、水の波とはまったく性質が異なる。水のソリトンは適当に水を乱してやれば消せるのに対して、こちらは途中を切断しない限り消すことはできない。2次元であっても「位相ソリトン」としてなら、孤立波を作れる場合がある。残念ながら、水は媒質としてあまりにも単純すぎるために、位相ソリトンを作ることはできない。ゴム紐にこれができて水にこれができない理由は、ゴム紐が「ひねれる」 のに対して水が「ひねれない」からだ。そういう意味でゴム紐のほうが水よりも「波の媒質として複雑」なのである。
(木口まこと)
図は全てJackson「非線形力学の展望」p15.